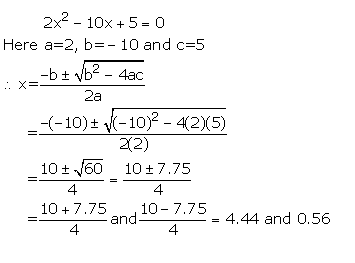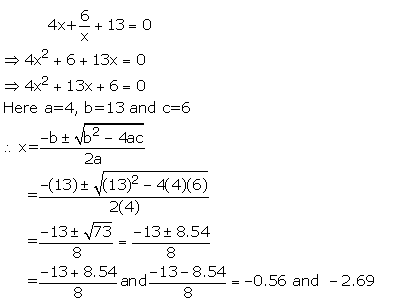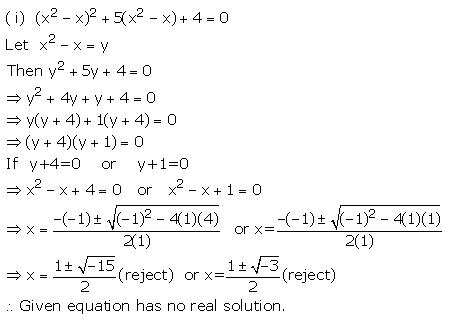Class 10 SELINA Solutions Maths Chapter 5 - Quadratic Equations
At TopperLearning, you get to learn through chapter-wise Selina solutions for your upcoming Class 10 ICSE board exams. In a quadratic equation, you have two as the highest power in a variable, and it takes a comprehensive understanding of the concept to help you solve roots and equations accurately.
All the solutions explained here at TopperLearning, are devised by professional subject matter experts according to the latest ICSE Class 10 Math Class 10 guidelines. The answers adhere to the exam pattern and marking scheme of the ICSE board so that students get a precise understanding of how to answer questions of different types. Moreover, te solutions are all numbered, similar to that of the main textbook. All you have to do is, maintain a fixed schedule for your Math practice before the exam and start learning online. TopperLearning, with the aim to make education affordable and accessible to all, offers solutions for free.
Once you are confident with the concepts in Quadratic Equations, start with your practice sessions using the ICSE Class 10 mock board exams. Also, you can follow a similar schedule for other chapters in Mathematics. Serving your best interests, you have the entire ICSE class 10 syllabus available at TopperLearning. Also, there are subject-wise ICSE Class 10 video lessons, Previous year’s question papers and sample papers available.
Quadratic Equations Exercise Ex. 5(A)
Solution 1(i)
(3x - 1)2 = 5(x + 8)
⇒ (9x2 - 6x + 1) = 5x + 40
⇒ 9x2 - 11x - 39 =0; which is of the form ax2 + bx + c = 0.
∴ Given equation is a quadratic equation.
Solution 1(ii)
5x2 - 8x = -3(7 - 2x)
⇒ 5x2 - 8x = 6x - 21
⇒ 5x2 - 14x + 21 =0; which is of the form ax2 + bx + c = 0.
∴ Given equation is a quadratic equation.
Solution 1(iii)
(x - 4)(3x + 1) = (3x - 1)(x +2)
⇒ 3x2 + x - 12x - 4 = 3x2 + 6x - x - 2
⇒ 16x + 2 =0; which is not of the form ax2 + bx + c = 0.
∴ Given equation is not a quadratic equation.
Solution 1(iv)
x2 + 5x - 5 = (x - 3)2
⇒ x2 + 5x - 5 = x2 - 6x + 9
⇒ 11x - 14 =0; which is not of the form ax2 + bx + c = 0.
∴ Given equation is not a quadratic equation.
Solution 1(v)
7x3 - 2x2 + 10 = (2x - 5)2
⇒ 7x3 - 2x2 + 10 = 4x2 - 20x + 25
⇒ 7x3 - 6x2 + 20x - 15 = 0; which is not of the form ax2 + bx + c = 0.
∴ Given equation is not a quadratic equation.
Solution 1(vi)
(x - 1)2 + (x + 2)2 + 3(x +1) = 0
⇒ x2 - 2x + 1 + x2 + 4x + 4 + 3x + 3 = 0
⇒ 2x2 + 5x + 8 = 0; which is of the form ax2 + bx + c = 0.
∴ Given equation is a quadratic equation.
Solution 2(i)
x2 - 2x - 15 = 0
For x = 5 to be solution of the given quadratic equation it should satisfy the equation.
So, substituting x = 5 in the given equation, we get
L.H.S = (5)2 - 2(5) - 15
= 25 - 10 - 15
= 0
= R.H.S
Hence, x = 5 is a solution of the quadratic equation x2 - 2x - 15 = 0.
Solution 2(ii)
2x2 - 7x + 9 = 0
For x = -3 to be solution of the given quadratic equation it should satisfy the equation
So, substituting x = 5 in the given equation, we get
L.H.S=2(-3)2 - 7(-3) + 9
= 18 + 21 + 9
= 48
≠ R.H.S
Hence, x = -3 is not a solution of the quadratic equation 2x2 - 7x + 9 = 0.
Solution 3
For x = 
to be solution of
the given quadratic equation it should satisfy the equation
So, substituting x = in the given
equation, we get
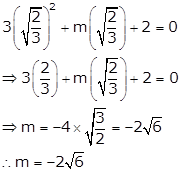
Solution 4
For x = 
and x = 1 to be
solutions of the given quadratic equation it should satisfy the equation
So, substituting x = and x = 1 in the
given equation, we get
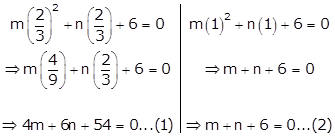
Solving equations (1) and (2) simultaneously,
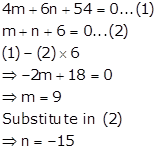
Solution 5
For x = 3 and x = -3 to be solutions of the given quadratic equation it should satisfy the equation
So, substituting x = 3 and x = -3 in the given equation, we get
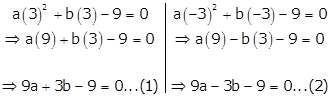
Solving equations (1) and (2) simultaneously,
Quadratic Equations Exercise Ex. 5(B)
Solution 1
Solution 2
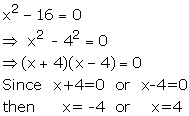
Solution 3
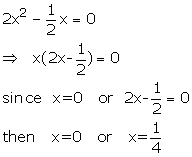
Solution 4
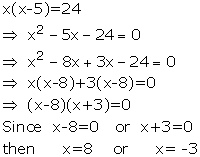
Solution 5
Solution 6
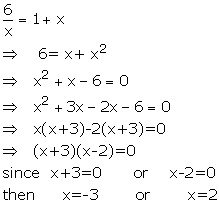
Solution 7
Solution 8
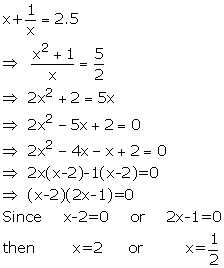
Solution 9
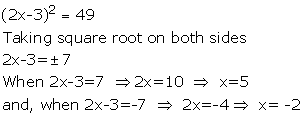
Solution 10
Solution 11
Solution 12
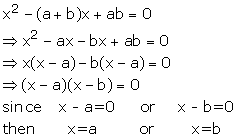
Solution 13
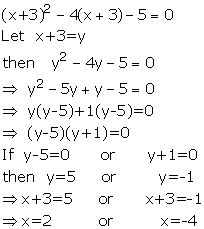
Solution 14
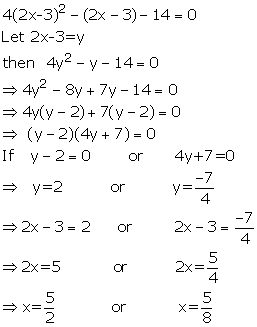
Solution 15
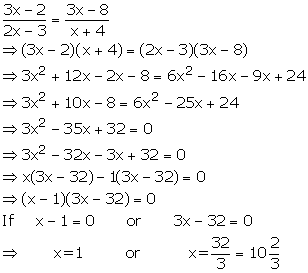
Solution 16
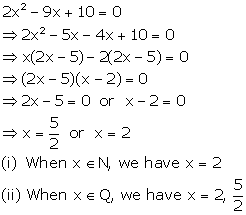
Solution 17
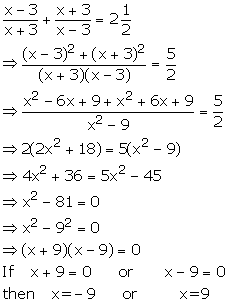
Solution 18
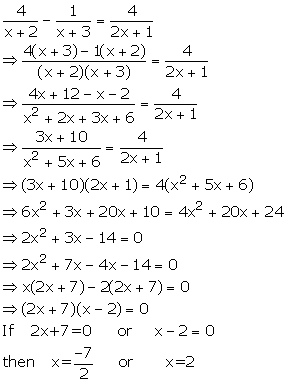
Solution 19
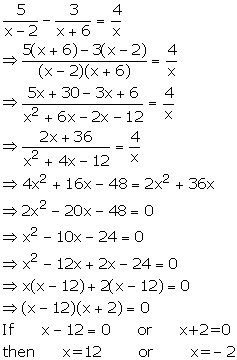
Solution 20
Solution 21
Solution 22(i)
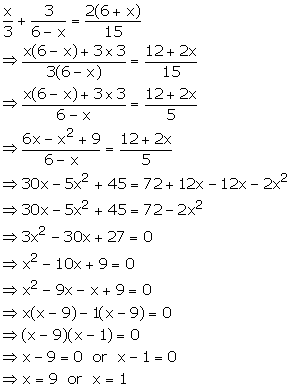
Solution 22(ii)
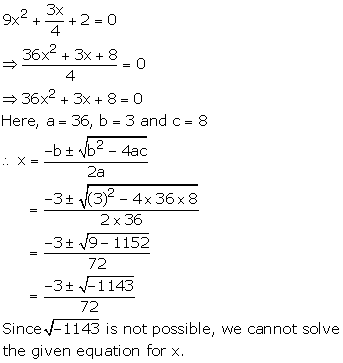
Solution 23
If a+1=0, then a = -1
Put this value in the given equation x2 + ax - 6 =0
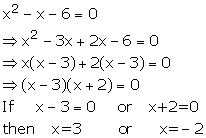
Solution 24
If a + 7 =0, then a = -7
and b + 10 =0, then b = - 10
Put these values of a and b in the given equation
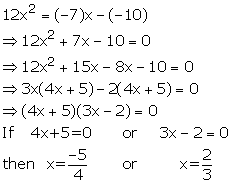
Solution 25
4(2x+3)2 - (2x+3) - 14 =0
Put 2x+3 = y
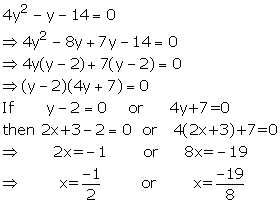
Solution 26
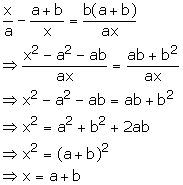
or x = -(a + b)
Solution 27
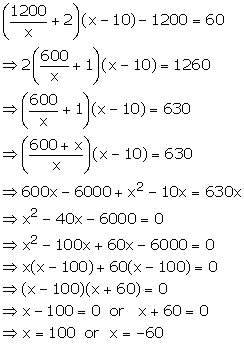
Quadratic Equations Exercise Ex. 5(C)
Solution 1
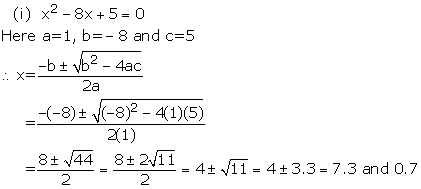
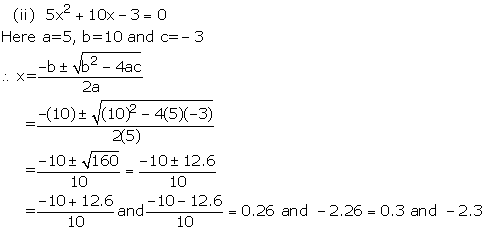
Solution 2(i)
Solution 2(ii)
Solution 2(iii)
4x2 - 5x - 3 = 0
Here, a = 4, b = -5 and c = -3
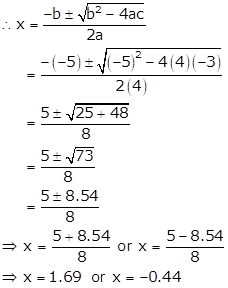
Solution 2(iv)
Solution 2(v)
Solution 3
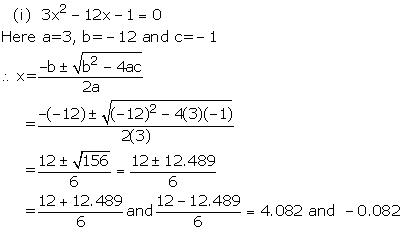
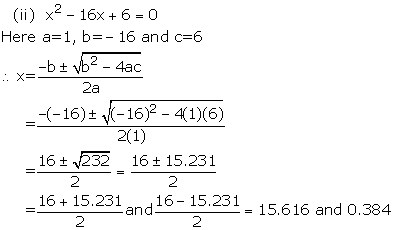
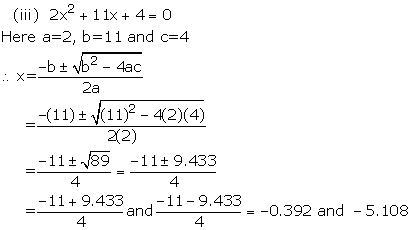
Solution 4
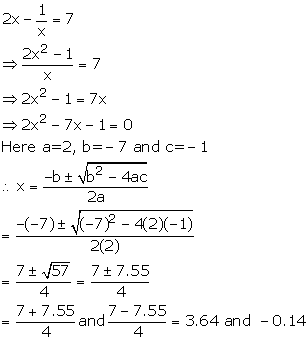
Solution 5
Consider the given equation:
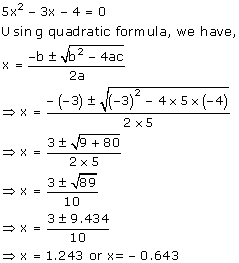
Solution 6
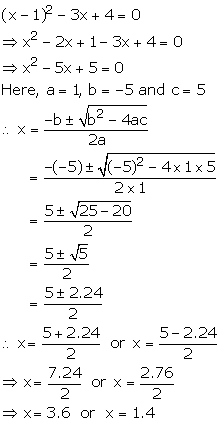
Solution 7
x2 - 3(x + 3) = 0
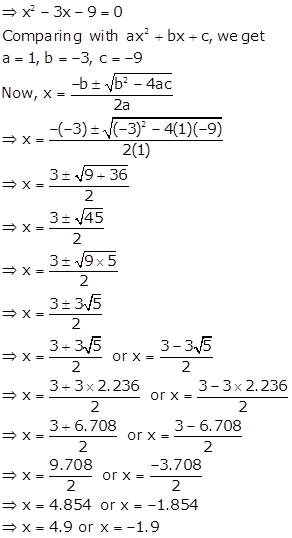
Quadratic Equations Exercise Ex. 5(D)
Solution 1
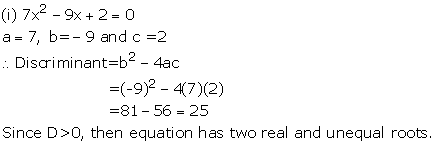
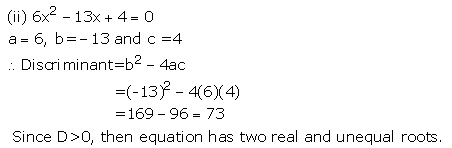
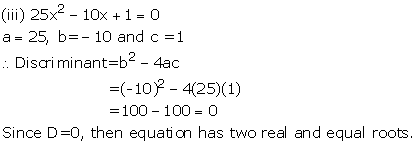
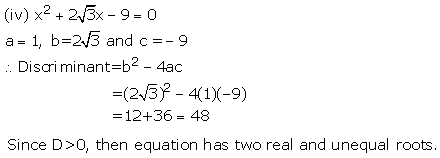
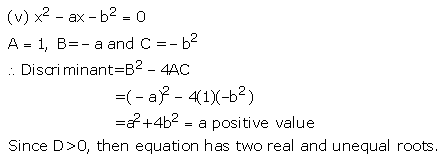
Solution 2(i)
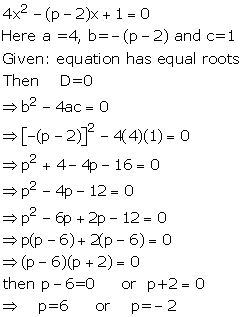
Solution 2(ii)
x2 + (p - 3)x + p = 0
Here, a = 1, b = (p - 3), c = p
Since, the roots are equal,
⇒ b2- 4ac = 0
⇒ (p - 3)2- 4(1)(p) = 0
⇒p2 + 9 - 6p - 4p = 0
⇒ p2- 10p + 9 = 0
⇒p2-9p - p + 9 = 0
⇒p(p - 9) - 1(p - 9) = 0
⇒ (p -9)(p - 1) = 0
⇒ p - 9 = 0 or p - 1 = 0
⇒ p = 9 or p = 1
Solution 3
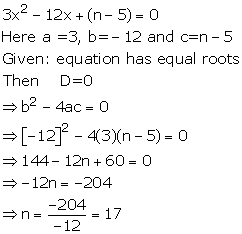
Solution 4
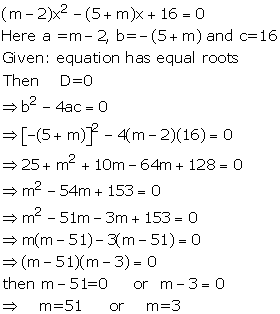
Solution 5
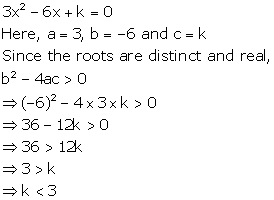
Solution 6
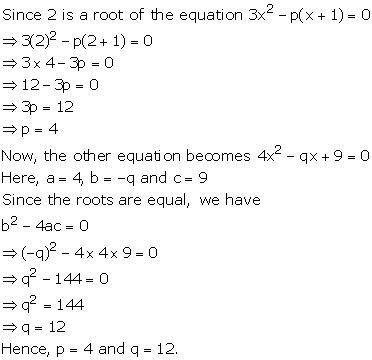
Quadratic Equations Exercise Ex. 5(E)
Solution 1
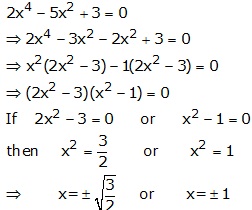
Solution 2
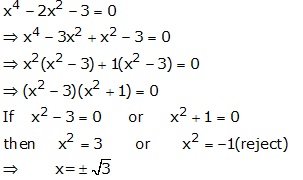
Solution 3
x4 - 10x2 + 9 = 0
⇒ x4 - 9x2 - x2 + 9 = 0
⇒ x2(x2 - 9) -1 (x2 - 9) = 0
⇒ (x2 - 9)( x2 - 1) = 0
If x2 - 9 = 0 or x2 - 1 = 0
⇒ x2 = 9 or x2 = 1
⇒ x = ±3 or x = ±1
Solution 4 (i)
Solution 4 (ii)
(x2 - 3x)2 - 16(x2 - 3x) - 36 = 0
Let x2 - 3x = y
Then y2 - 16y - 36 = 0
⇒ y2 - 18y + 2y - 36 = 0
⇒ y(y - 18) + 2(y - 18) = 0
⇒ (y - 18) (y + 2) = 0
If y - 18 = 0 or y + 2 = 0
⇒ x2 - 3x - 18 = 0 or x2 - 3x + 2 = 0
⇒ x2 - 6x + 3x - 18 = 0 or x2 - 2x - x + 2 = 0
⇒ x(x - 6) +3(x - 6) = 0 or x(x - 2) -1(x - 2) = 0
⇒ (x - 6) (x + 3) = 0 or (x - 2) (x - 1) = 0
If x - 6 = 0 or x + 3 = 0 or x - 2 = 0 or x - 1 = 0
then x = 6 or x = -3 or x = 2 or x = 1
Solution 5
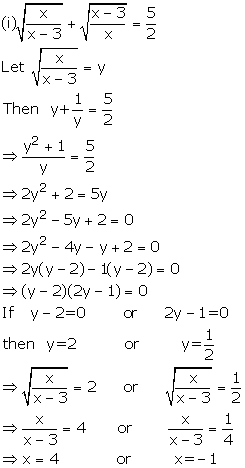
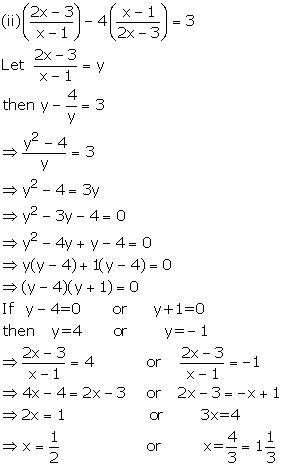
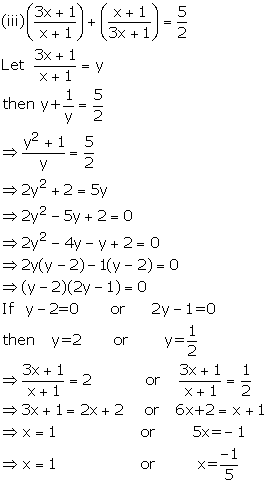
Solution 6
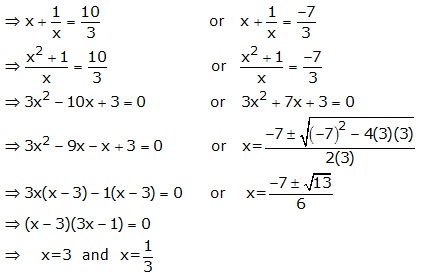
Solution 7
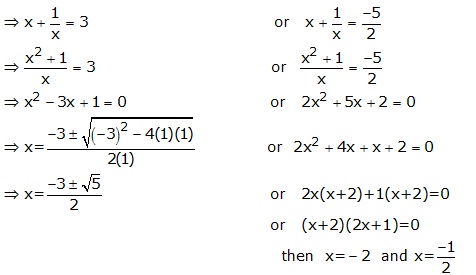
Solution 8
Solution 9
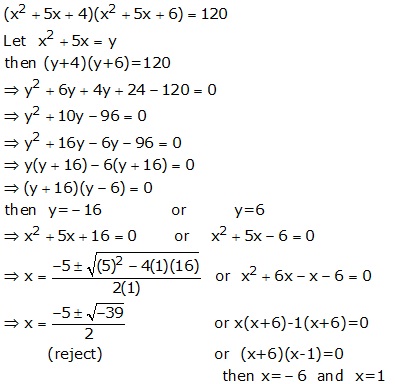
Solution 10
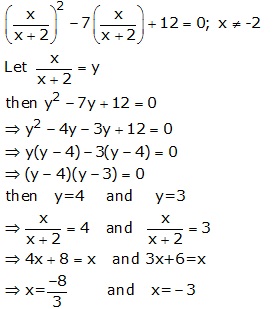
Solution 11
∴ Given equation reduces to
⇒ 2y2 - 3 = 5y
⇒ 2y2 - 5y - 3 = 0
⇒ 2y2 - 6y + y - 3 = 0
⇒ 2y(y - 3) + 1(y - 3) = 0
⇒ (y - 3)(2y + 1) = 0
⇒ y = 3 and 
When, y = 3
⇒ 2x - 1 = 3x + 9
⇒ x = -10
When,
⇒ 4x - 2 = -x - 3
Solution 12
(i)
p2x2 - (p2 - q2)x - q2 = 0
Comparing p2x2 - (p2 - q2)x - q2 = 0 with ax2 + bx + c = 0, we get:
a = p2, b = -(p2 - q2) and c = -q2
So,
(ii)
abx2 + (b2 - ac)x - bc = 0
The quadratic formula for the quadratic equation ax2 + bx + c = 0 is given by:
Quadratic Equations Exercise Ex. 5(F)
Solution 1
Given 
i.e 
So, the given quadratic equation becomes
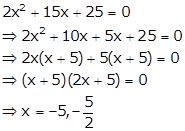
Hence, the values of x are 
and
.
Solution 2
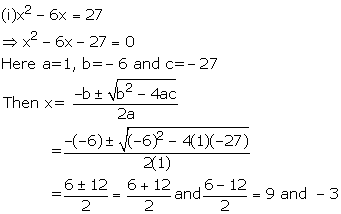
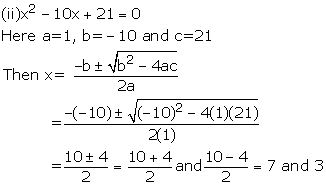
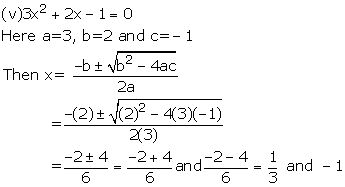
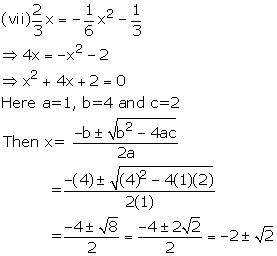
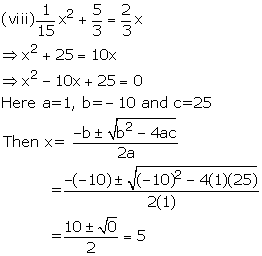
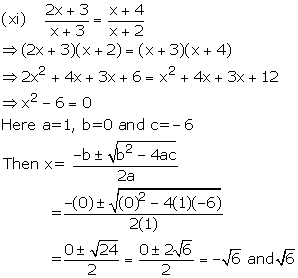
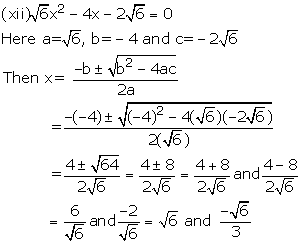
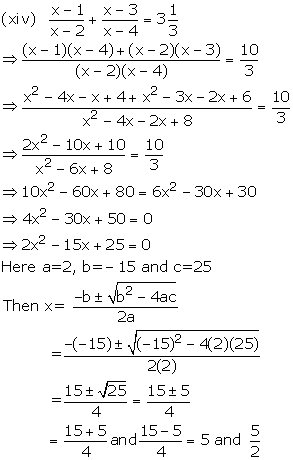
Solution 3
(i) Given quadratic equation is 
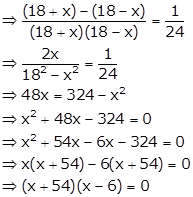
or 
But as x > 0, so x can't be negative.
Hence, x = 6.
(ii) Given quadratic equation is 
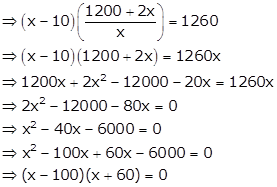
or 
But as x < 0, so x can't be positive.
Hence, 
Solution 4
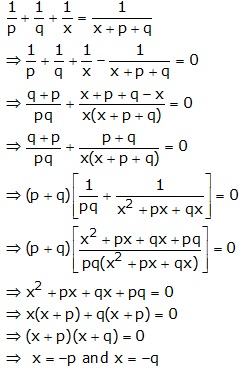
Solution 5
Given quadratic equation is 
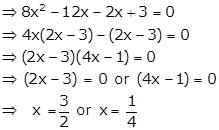
(i) When 
the equation has no roots
(ii) When 
the roots of are
or 
Solution 6
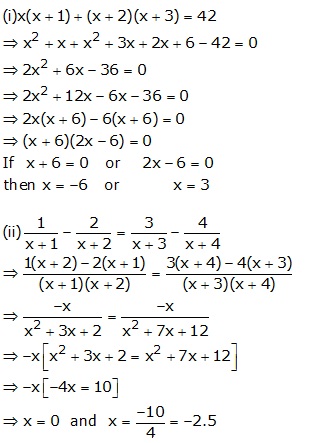
Solution 7
Given quadratic equation is 
Using quadratic formula,
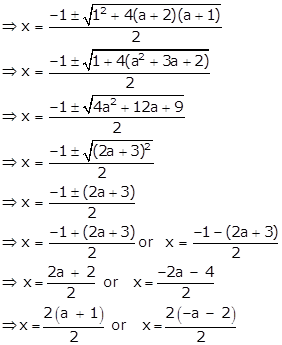
⇒ x = a + 1 or x = -a - 2 = -(a + 2)
Solution 8
Given quadratic equation is 
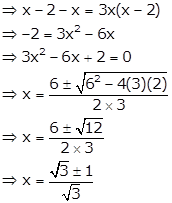
Since, m and n are roots of the equation, we have
and 
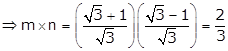
Hence, 
.
Solution 9
Given quadratic equation is 
…. (i)
One of the roots of (i) is 
, so it satisfies (i)
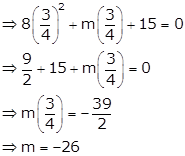
So, the equation (i) becomes 
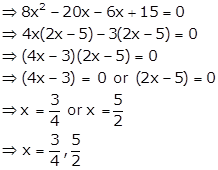
Hence, the other root is
.
Solution 10
Given quadratic equation is 
…. (i)
One of the roots of (i) is -3, so it satisfies (i)
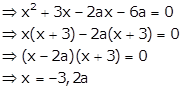
Hence, the other root is 2a.
Solution 11
Given quadratic equation is 
….. (i)
Also, given 
and 
and 
So, the equation (i) becomes
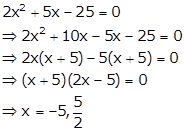
Hence, the solution of given quadratic equation are and.
Solution 12
Given quadratic equation is 
…. (i)
The quadratic equation has equal roots if its discriminant is zero
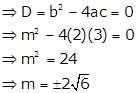
When 
, equation (i) becomes
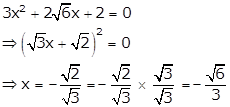
When 
, equation (i) becomes
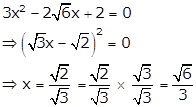
∴ x = 
Solution 13
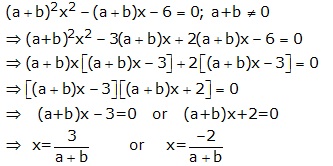
Solution 14
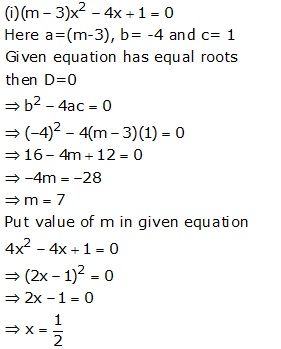
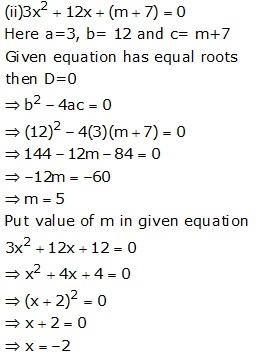
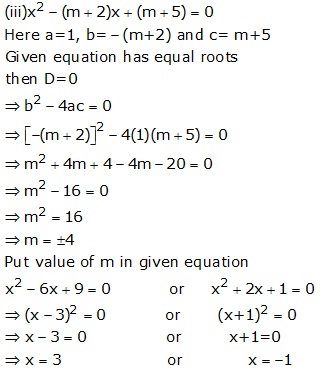
Solution 15
Solution 16
Consider the given equation:
Solution 17
Given quadratic equation is 
The quadratic equation has real and equal roots if its discriminant is zero.
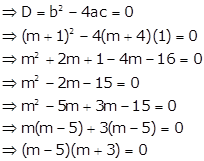
or 
Solution 18
Given quadratic equation is 
…. (i)
The quadratic equation has real roots if its discriminant is greater than or equal to zero
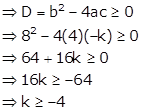
Hence, the given quadratic equation has real roots for
.
Solution 19
(i) Given quadratic equation is 
D = b2 - 4ac =
= 25 - 24 = 1
Since D > 0, the roots of the given quadratic equation are real and distinct.
Using quadratic formula, we have
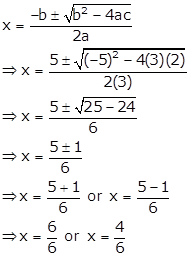
or 
(ii) Given quadratic equation is 
D = b2 - 4ac =
= 16 - 20 = - 4
Since D < 0, the roots of the given quadratic equation does not exist.
Solution 20
Since, -2 is a root of the equation 3x2 + 7x + p = 1.
⇒ 3(-2)2 + 7(-2) + p = 1
⇒ 12 - 14 + p = 1
⇒ p = 3
The quadratic equation is x2 + k(4x + k - 1) + p = 0
i.e. x2 + 4kx + k2 - k + 3 = 0
Comparing equation x2 + 4kx + k2 - k + 3 = 0 with ax2 + bx + c = 0, we get
a = 1, b = 4k and c = k2 - k + 3
Since, the roots are equal.
⇒ b2 - 4ac = 0
⇒ (4k)2 - 4(k2 - k + 3) = 0
⇒ 16k2 - 4k2 + 4k - 12 = 0
⇒ 12k2 + 4k - 12 = 0
⇒ 3k2 + k - 3 = 0
By quadratic formula, we have
